The Discovery of the Pythagorean Theory
During his stay in Egypt, Pythagoras studied with engineers who constructed the pyramids, they were called ‘rope stretchers’. The rope stretchers had a special secret they used for constructing pyramids and other structures. This was a circular rope with 12 uniformly spaced knots, when the knots were arranged in measurements of 3-4-5, a right angle would be instantly formed, they pegged the three points to the ground and this made it possible to lay foundations for their structures accurately.
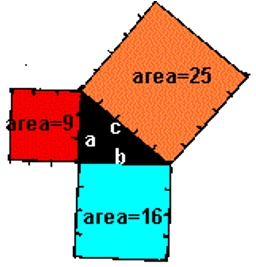
Pythagoras was so obsessed with the Egyptian rope stretchers after returning home that he spent many years thinking about it and the logic behind it. He soon discovered that the 3-4-5 triangle held a great deal of Mathematics that he equated to magical power (Diggins, 1965, pp. 78). One day as he was making diagrams on the sand, he discovered that if a square is drawn from each of the three sides of the 3-4-5 triangle, the sum of the area of the two smaller squares was equal to the area of the largest square, as shown below:
He also observed that if the distances were multiplied by a common factor, say 2, a right triangle was formed, i.e.
62 + 82 = 102
36 + 64 = 100
122 + 162 = 202
144 + 256 = 400
Upon making this discovery, Pythagoras declared it as a revelation from the god Apollo, believed by many to be his father. When he made public the findings, he used the arbitrary terms of a and b for the shorter sides and c for the longest side which he called the hypotenuse. The Pythagorean Theorem can thus be stated as:
a2 + b2 = c2, where a and b represent the lengths of the sides that form the right angle, while c is the length of the longest side (hypotenuse), opposite the right angle.
In other words, the theory can be stated as “in any right triangle (right-angled triangle), the area of the square whole side in the hypotenuse (longest side or the side opposite the right angle) is equivalent to the sum of the areas of the squares whose sides are the two shorter ones (the two sides that meet to form a right angle)” (NASA, 2009, para. 3).
The Pythagorean Theorem
In its elementary form, the Pythagorean Theorem relates the three sides of a triangle and makes it possible to find any missing lengths in a right triangle. The formula a2 + b2 = c2 shows two basic facets of this theorem: it is both a statement relating the lengths and areas. Tobias Dantzig referred to this aspect as areal and metric dimensions. Some proofs of this theorem are founded on one aspect, some upon the other, hence, Pythagoras’ Theorem is based on geometry and algebra, a link made clear originally by Descartes, and today broadened into other fields of mathematics.
The Pythagorean Theorem has been adapted into other areas outside of its original application such as many dimensional Euclidian spaces, to those that are non-Euclidian and non-triangular shapes.
Other Forms of the Pythagorean Theorem
As shown earlier, the Pythagorean Theorem is given by the equation
a2 + b2 = c2,
the length of the hypotenuse is found making c the subject of the formula, i.e.
![]()
if c is known, we can find the length of any of the two shorter sides, i.e.
![]()
Similarly, the length a is found as:
![]()
(Weisstein, 2010, para. 8)
Proofs of the Theory
The Pythagorean Theorem is probably one with the highest number of known proofs (more than 370), with more under consideration. Some of the most common proofs are shown below:
Use of Similar Triangles
This is founded on the congruence of the two triangles, i.e. the ratio of any two matching sides of similar triangles is equal irrespective of their size. Consider the triangle below:

ACH and ABC are congruent as they both have a right angle and also have a similar angle (marked θ). Therefore, by similarity:
![]()
The first relation compares the cosine of each angle θ while the second compares the sine rule.
Cross-multiplication gives the following:
![]()
Adding up the two equations gives:
![]()
Hence,
![]()
(Bogolmny, 2010, para. 14)
Algebraic Proof
The theorem can be proved using four identical right triangles as shown below:

These four triangles are identical since the area of a triangle is given by ½ ab, the area of the small square is (b – a)2, the area of the larger square of side c is, therefore:
therefore ![]()
But the area of the larger square is also given by c2, therefore: ![]()
There exist many proofs to this theorem, others are Euclid’s proof, proof by re-arrangement, proof using differentials, among many others. The theory has also been used to deduce several mathematical generalizations, e.g. the cosine law, and in several trigonometric identities.
Reference List
Bogolmny, A. (2010). Pythagorean Theorem and its many proofs from Interactive Mathematics Miscellany and Puzzles. Web.
Diggins, J. E. (1965). String, Straight-Edge, & Shadow, The Story Of Geometry. New York: The Viking Press.
NASA. (2006). Pythagorean Theorem. Web.
Weisstein, E. W. (2010). Pythagorean Theorem. Web.