For the purposes of this discussion, two functions were chosen at random. Their formulas are given below:
In order to maintain logical consistency and brevity, in this post, the functions are denoted as E and H. First, it should be noted that both equations are exponential: the graphs of the functions are shown in the Figures below. The graph of the function E is shown in red on the left, while the black on the right describes the functional dependence of H.
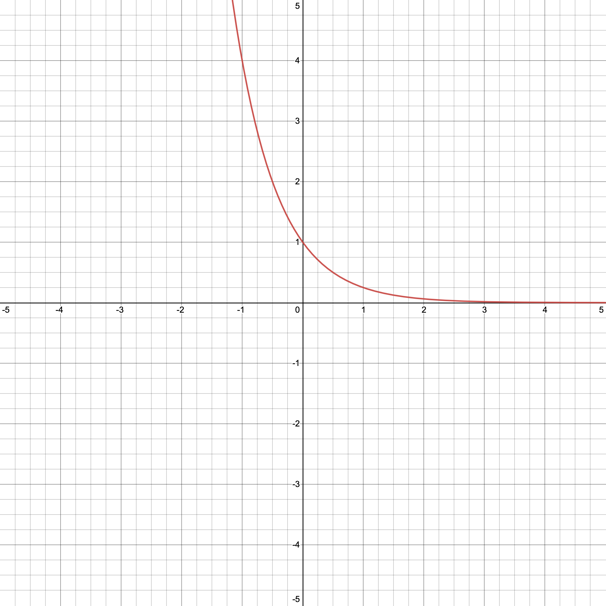
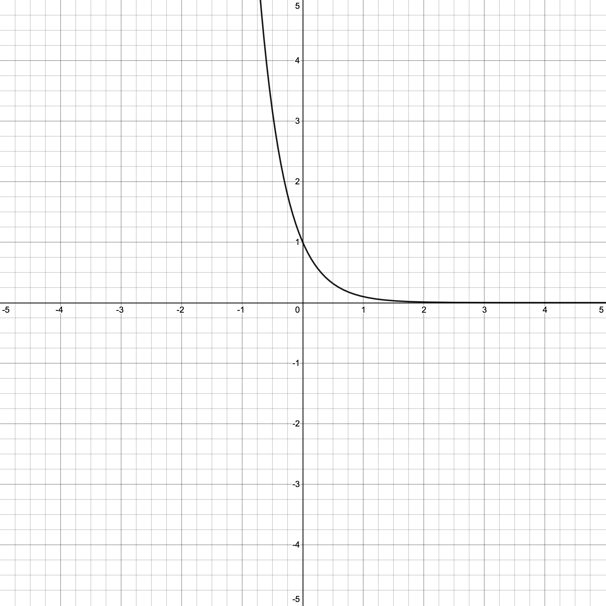
It is easy to see that the graphs have a broadly similar appearance: it is a decreasing function over the entire domain, which slows down the rate of decline considerably as it approaches the abscissa axis. Moreover, both graphs can never cross the horizontal axis at once due to the impossibility of the exponential function being equal to zero. At the same time, both functions cross the ordinate axis at (0,1) because only in the zero degrees can the exponent be equal to one. However, it is not difficult to emphasize the visual difference between the functions: E, unlike H, has a more expanded form. For example, at x = -1, E has a value of 4, while H equals 10.
The similarity of the two functions lies in the definition of the range: each of them extends over the entire abscissa axis or, more precisely, has a range (-∞,∞). The same is true for the range, which in both cases is (0,∞). Moreover, both E and H have the same horizontal asymptote equation: y=0. The existence of precisely such an equation — one should say, the only asymptote at all — is due to the functional requirements for the equation, namely, the impossibility of the function being equal to zero. Moreover, as can be seen, the functions do not affect the region of negative values. The requirement for an exponential function also justifies this property: no degree can force a function to be equal to a negative value. Finally, in order to find an inverse function, you must swap the variables and then solve the equation concerning the dependent variable. Here is how this should be done for the function E:
In that case, the inverse function for H will have almost the same form:
